EJERCICIO 32

Description

Problema 21.104 del Young – Freedman. Decimosegunda Edición. Página 748.

Un disco delgado con un agujero circular en el centro, llamado corona circular, tiene un radio interior R₁ y un radio exterior R₂ (figura). El disco tiene una densidad superficial de carga uniforme y positiva σ en su superficie. a) Determine la carga eléctrica total en la corona circular. b) La corona circular se encuentra en el plano y z, con su centro en el origen. Para un punto arbitrario en el eje x (el eje de la corona circular), encuentre la magnitud y la dirección del campo eléctrico E. Considere puntos arriba y abajo de la corona circular en la figura. c) Demuestre que en puntos sobre el eje x que estén suficientemente cerca del origen, la magnitud del campo eléctrico es aproximadamente proporcional a la distancia entre el centro de la corona circular y el punto. ¿Qué tan cerca es “suficientemente cerca”? d) Una partícula puntual con masa m y carga negativa – q tiene libertad de movimiento a lo largo del eje x (pero no puede apartarse del eje). Originalmente, la partícula está en reposo en x = 0.01 R₁ y luego se libera. Encuentre la frecuencia de oscilación de la partícula. (Sugerencia: La corona circular permanece estacionaria.)

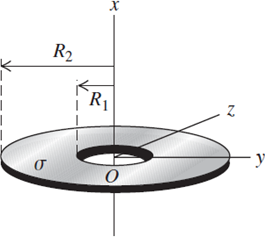
A thin disk with a circular hole at its centre, called an annulus, has inner radius R₁ and outer radius R₂ (Fig.). The disk has a uniform positive surface charge density σ on its surface. (a) Determine the total electric charge on the annulus. (b) The annulus lies in the y z-plane, with its centre at the origin. For an arbitrary point on the x-axis (the axis of the annulus), find the magnitude and direction of the electric field E. Consider points both above and below the annulus in Fig. (c) Show that at points on the x-axis that are sufficiently close to the origin, the magnitude of the electric field is approximately proportional to the distance between the centre of the annulus and the point. How close is ‘sufficiently close’? (d) A point particle with mass m and negative charge – q is free to move along the x-axis (but cannot move off the axis). The particle is originally placed at rest at x = 0.01 R₁ and released. Find the frequency of oscillation of the particle. (Hint: The annulus is held stationary.)